BYOM function simplefun.m (the model as explicit equations)

Syntax: Xout = simplefun(t,X0,par,c,glo)

This function calculates the output of the model system. It is linked to the script files byom_bioconc_extra.m and byom_bioconc_start.m. As input, it gets:

Note: glo is now an input to this function rather than a global. This makes the code faster (though only very little when using simplefun).

Time t is handed over as a vector, and scenario name c as single number, by call_deri.m (you do not have to use them in this function). Output Xout (as matrix) provides the output for each state at each t.

Copyright (c) 2012-2021, Tjalling Jager, all rights reserved.
This source code is licensed under the MIT-style license found in the
LICENSE.txt file in the root directory of BYOM.

Contents

Start

Note that, in this example, variable c (the scenario identifier) is not used in this function. The treatments differ in their initial exposure concentration that is set in X0mat. Also, the structure glo is not used here.

function Xout = simplefun(t,X0,par,c,glo)

Unpack initial states

The state variables enter this function in the vector _X_0.

Cw0 = X0(1); % state 1 is the external concentration at t=0
Ci0 = X0(2); % state 2 is the internal concentration at t=0

Unpack parameters

The parameters enter this function in the structure par. The names in the structure are the same as those defined in the byom script file. The 1 between parentheses is needed as each parameter has 5 associated values.

kd   = par.kd(1);   % degradation rate constant, d-1
ke   = par.ke(1);   % elimination rate constant, d-1
Piw  = par.Piw(1);  % bioconcentration factor, L/kg
Ct   = par.Ct(1);   % threshold external concentration that stops degradation, mg/L

Calculate the model output

This is the actual model, specified as explicit function(s):

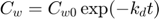
$$ C_w=C_{w0} \exp(-k_d t) $$

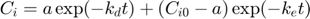
$$ C_i= a \exp(-k_d t) + (C_{i0}-a) \exp(-k_e t) $$

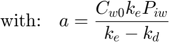
$$ \textrm{with:} \quad a= \frac{C_{w0} k_e P_{iw}}{k_e-k_d} $$

Note: this function is not completely identical to the solution of the system of ODE's. Here, I ignore the stop in degradation, which would require quite some fiddling around. Watch out that this solution is only valid when ke is NOT equal to kd!

Cw = Cw0 * exp(-kd*t); % concentration in water

a  = Cw0 * ke * Piw/(ke-kd); % this factor occurs twice in the solution
Ci = a*exp(-kd*t) + (Ci0 - a) * exp(-ke*t); % internal concentration

Xout = [Cw Ci]; % combine them into a matrix


Published with MATLAB® R2021b